HTB - Weak RSA

Overview

Challenge	Find the easy pass
Rank	Easy
Time	-
Category	Crypto

Enumeration

All we have is:

1. flag.enc, the encrypted flag in a binary file
2. key.pub, the public key used to encrypt it (which we know its an RSA key).

[Wikipedia] RSA (Rivest–Shamir–Adleman) is a public-key cryptosystem, one of the oldest that is widely used for secure data transmission. In a public-key cryptosystem, the encryption key is public and distinct from the decryption key, which is kept secret (private). An RSA user creates and publishes a public key based on two large prime numbers, along with an auxiliary value. The prime numbers are kept secret. Messages can be encrypted by anyone, via the public key, but can only be decoded by someone who knows the private key. The security of RSA relies on the practical difficulty of factoring the product of two large prime numbers, the “factoring problem”. Breaking RSA encryption is known as the RSA problem. There are no published methods to defeat the system if a large enough key is used.

We can use pycryptodome lib to load the RSA key and extract its values. Since it is a public key, we expect to get N, the public modulus, and e, the public exponent:

pycryptodome did not work, but pycryptodomex worked –> Documentation

>>> from Crypto.PublicKey import RSA
>>> def get_pubkey(f):
...     with open(f) as pub:
...             key = RSA.importKey(pub.read())
...     return (key.n, key.e)
...
>>> N, e = get_pubkey('./key.pub')
>>> print(N)
573177824579630911668469272712547865443556654086190104722795509756891670023259031275433509121481030331598569379383505928315495462888788593695945321417676298471525243254143375622365552296949413920679290535717172319562064308937342567483690486592868352763021360051776130919666984258847567032959931761686072492923
>>> print(e)
68180928631284147212820507192605734632035524131139938618069575375591806315288775310503696874509130847529572462608728019290710149661300246138036579342079580434777344111245495187927881132138357958744974243365962204835089753987667395511682829391276714359582055290140617797814443530797154040685978229936907206605

Usually the public exponent, e, is a much smaller number, with 0x1001 being a very common choice. So this is something very interesting to research.

Solution

Finding the vulnerability

Since e is very large, it can lead to a small private exponent, d. However, a small d leads to a broken RSA encryption (as described in this paper).

Exploitation

Loading key and ciphertext

We will use the above function, get_pubkey(), to get the public key values, and we will write another function, get_ciphertext(), to load the ciphertext and convert it to a number so we can work with it:

>>> def get_ciphertext(f):
...     with open(f, 'rb') as ct:
...             return bytes_to_long(ct.read())

Performing Wiener’s attack

There is a Python module, owiener, that implements the Wiener attack:

RSA Wiener’s attack is a method used to break the security of RSA encryption when the private key is vulnerable due to a specific weakness. RSA is a widely used encryption algorithm that relies on the difficulty of factoring the product of two large prime numbers. In simple terms, it’s hard to figure out the original prime numbers from the result of multiplying them.

Wiener’s attack specifically targets situations where the private key’s value is too small. The attack exploits vulnerabilities in cases where the private exponent (a part of the private key) is much smaller than it should be, making it easier for an attacker to calculate and discover the private key.

d = owiener.attack(e, N)

Decrypting RSA

Now that we have the private exponent, we have everything we need to decrypt RSA and get our plaintext:

def decrypt_rsa(N, e, d, ct):
	pt = pow(ct, d, N)
	return long_to_bytes(pt)

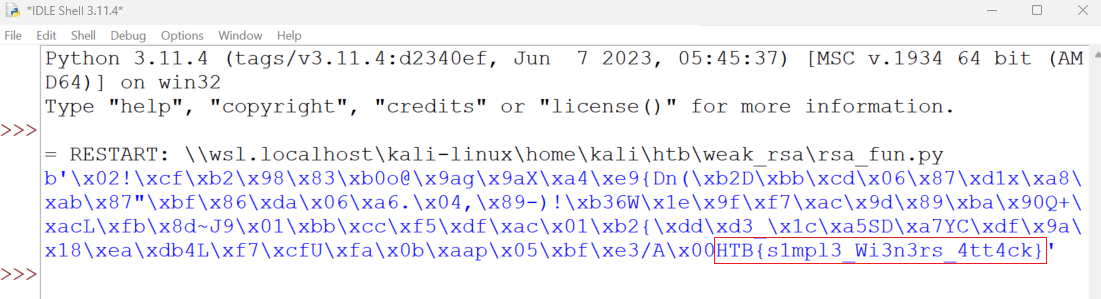
Getting the flag

A final summary of all that was said above:

1. We have extracted the public values from the key.
2. We have recovered the private exponent d through the Wiener attack.
3. We have decrypted the ciphertext.

This recap can be represented by code with the pwn() function:

from Cryptodome.PublicKey import RSA
from Cryptodome.Util.number import bytes_to_long, long_to_bytes
import owiener

def get_pubkey(f):
	with open(f) as pub:
		key = RSA.importKey(pub.read())
	return (key.n, key.e)

N, e = get_pubkey('./key.pub')

def get_ciphertext(f):
	with open(f, 'rb') as ct:
		return bytes_to_long(ct.read())

d = owiener.attack(e, N)

def decrypt_rsa(N, e, d, ct):
	pt = pow(ct, d, N)
	return long_to_bytes(pt)

def pwn():
	N, e = get_pubkey('./key.pub')
	ct = get_ciphertext('./flag.enc')
	d = owiener.attack(e, N)
	flag = decrypt_rsa(N, e, d, ct)
	print(flag)

if __name__ == '__main__':
	pwn()